Abstract
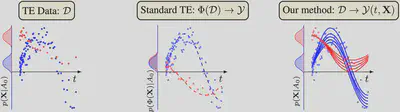
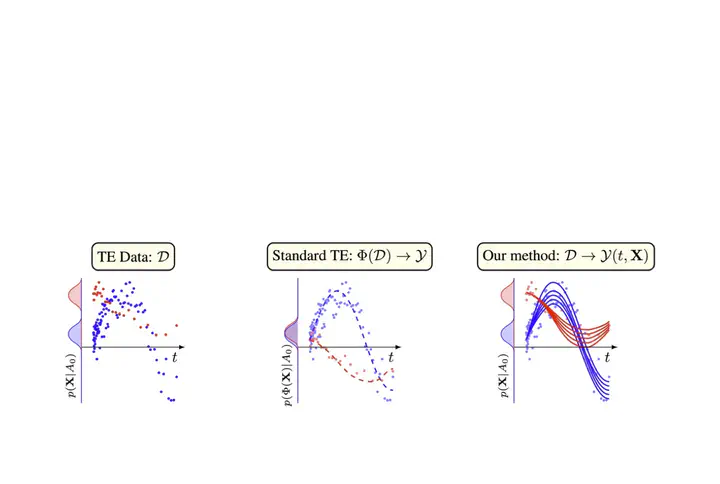
Inferring unbiased treatment effects has received widespread attention in the machine learning community. In recent years, our community has proposed numerous solutions in standard settings, high-dimensional treatment settings, and even longitudinal settings. While very diverse, the solution has almost always relied on neural networks for inference and simultaneous correction of assignment bias. New approaches typically build on top of previous approaches by proposing new (or refined) architectures and learning algorithms. However, the end result—a neural-network-based inference machine—remains unchallenged. In this paper, we introduce a different type of solution in the longitudinal setting: a closed-form and human-readable ordinary differential equation (ODE). While we still rely on continuous optimization to learn an ODE, the resulting inference machine is no longer a neural network. Doing so yields several advantages such as interpretability, irregular sampling, and a different set of identification assumptions. Above all, we consider the introduction of a completely new type of solution to be our most important contribution as it may spark entirely new innovations in treatment effects in general. We facilitate this by formulating our contribution as a framework that can transform any ODE discovery method into a treatment effects method.
Paper Key Figure