Abstract
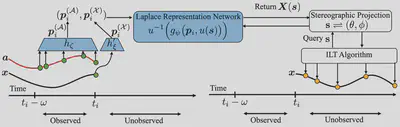
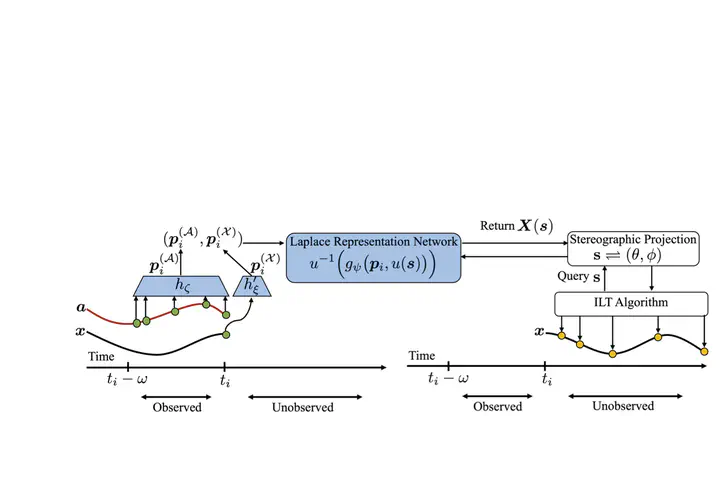
Many real-world offline reinforcement learning (RL) problems involve continuous-time environments with delays. Such environments are characterized by two distinctive features; firstly, the state $x(t)$ is observed at irregular time intervals, and secondly, the current action $a(t)$ only affects the future state $x(t + g)$ with an unknown delay $g > 0$. A prime example of such an environment is satellite control where the communication link between earth and a satellite causes irregular observations and delays. Existing offline RL algorithms have achieved success in environments with irregularly observed states in time or known delays. However, environments involving both irregular observations in time and unknown delays remains an open and challenging problem. To this end, we propose Neural Laplace Control, a continuous-time model-based offline RL method that combines a Neural Laplace dynamics model with a model predictive control (MPC) planner—and is able to learn from a offline dataset sampled with irregular time intervals from an environment that has a inherent unknown constant delay. We show experimentally on continuous-time delayed environments it is able to achieve near expert policy performance.
Virtual Presentation
Paper Key Figure