Abstract
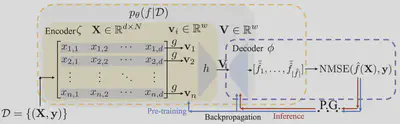
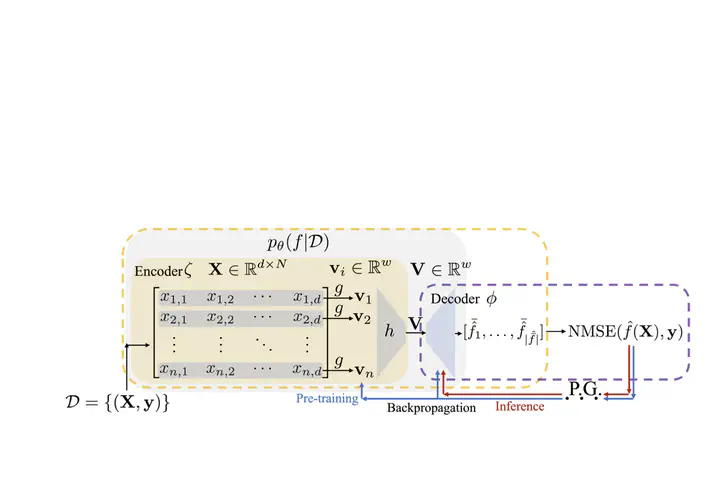
Symbolic regression (SR) aims to discover concise closed-form mathematical equations from data, a task fundamental to scientific discovery. However, the problem is highly challenging because closed-form equations lie in a complex combinatorial search space. Existing methods, ranging from heuristic search to reinforcement learning, fail to scale with the number of input variables. We make the observation that closed-form equations often have structural characteristics and invariances (e.g. the commutative law) that could be further exploited to build more effective symbolic regression solutions. Motivated by this observation, our key contribution is to leverage pre-trained deep generative models to capture the intrinsic regularities of equations, thereby providing a solid foundation for subsequent optimization steps. We show that our novel formalism unifies several prominent approaches of symbolic regression and offers a new perspective to justify and improve on the previous ad hoc designs, such as the usage of cross-entropy loss during pre-training. Specifically, we propose an instantiation of our framework, Deep Generative Symbolic Regression (DGSR). In our experiments, we show that DGSR achieves a higher recovery rate of true equations in the setting of a larger number of input variables, and it is more computationally efficient at inference time than state-of-the-art RL symbolic regression solutions.
Paper Key Figure