Active Observing in Continuous-time Control

Abstract

The control of continuous-time environments while actively deciding when to take costly observations in time is a crucial yet unexplored problem, particularly relevant to real-world scenarios such as medicine, low-power systems, and resource management. Existing approaches either rely on continuous-time control methods that take regular, expensive observations in time or discrete-time control with costly observation methods, which are inapplicable to continuous-time settings due to the compounding discretization errors introduced by time discretization. In this work, we are the first to formalize the continuous-time control problem with costly observations. Our key theoretical contribution shows that observing at regular time intervals is not optimal in certain environments, while irregular observation policies yield higher expected utility. This perspective paves the way for the development of novel methods that can take irregular observations in continuous-time control with costly observations. We empirically validate our theoretical findings in various continuous-time environments, including a cancer simulation, by constructing a simple initial method to solve this new problem, with a heuristic threshold on the variance of reward rollouts in an offline continuous-time model-based model predictive control (MPC) planner. Although determining the optimal method remains an open problem, our work offers valuable insights and understanding of this unique problem, laying the foundation for future research in this area.

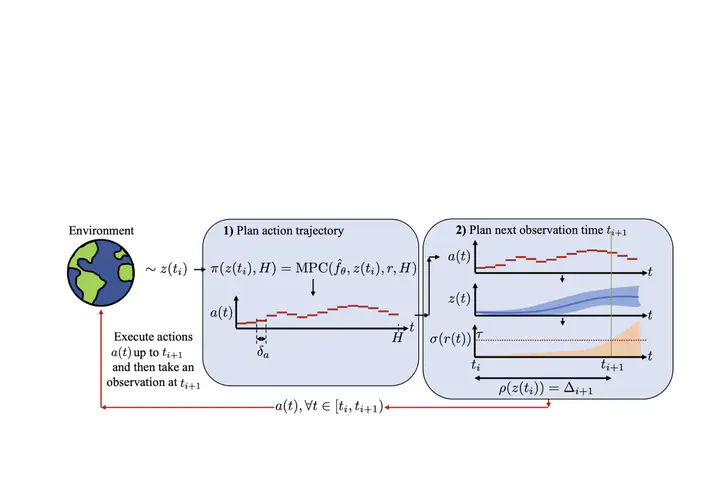
Paper Key Figure

Block diagram of Active Observing Control. An uncertainty-aware dynamics model $\hat{f}$ is learned from an offline dataset $\mathcal{D}$ of state-action trajectories. At run-time, planning consists of two steps: 1) The actions are determined by a Model Predictive Control (MPC) Planner, and 2) the determined action trajectory $a$ is forward simulated to provide uncertainty $\sigma(r(t))$ on the planned path reward. We determine the continuous time $t_{i+1}$ to execute the action plan $a$ up to, such that $\sigma(r(t)) < \tau$. We then execute $a(t)$ $\forall t \in [t_i, t_{i+1})$ up until the time to take the next observation $z(t)$ at.

Samuel Holt

PhD Researcher