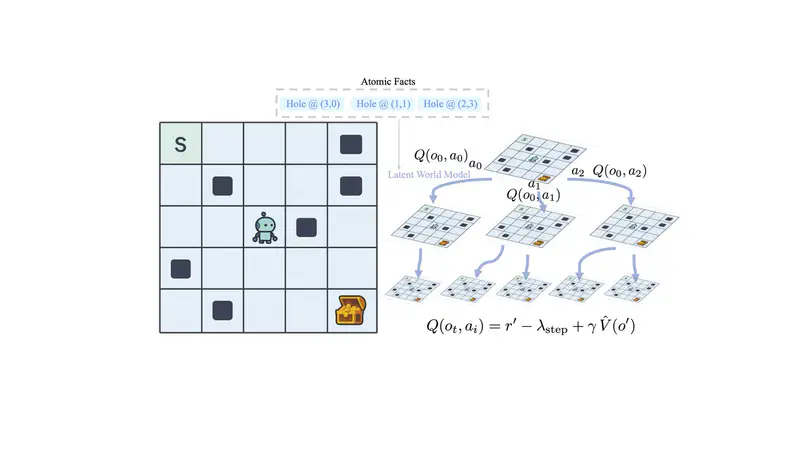
Large Language Models (LLMs) are increasingly capable but often require significant guidance or extensive interaction history to perform effectively in complex, interactive environments. Existing methods may struggle with adapting to new information or efficiently utilizing past experiences for multi-step reasoning without fine-tuning. We introduce a novel LLM agent framework that enhances planning capabilities through in-context learning, facilitated by atomic fact augmentation and a recursive lookahead search. Our agent learns to extract task-critical “atomic facts” from its interaction trajectories. These facts dynamically augment the prompts provided to LLM-based components responsible for action proposal, latent world model simulation, and state-value estimation. Planning is performed via a depth-limited lookahead search, where the LLM simulates potential trajectories and evaluates their outcomes, guided by the accumulated facts and interaction history. This approach allows the agent to improve its understanding and decision-making online, leveraging its experience to refine its behavior without weight updates. We provide a theoretical motivation linking performance to the quality of fact-based abstraction and LLM simulation accuracy. Empirically, our agent demonstrates improved performance and adaptability on challenging interactive tasks, achieving more optimal behavior as it accumulates experience, showcased in tasks such as TextFrozenLake and ALFWorld.

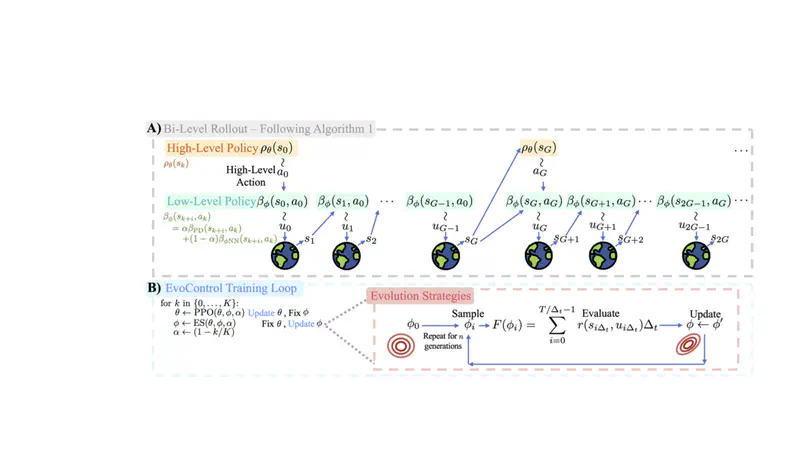
High-frequency control in continuous action and state spaces is essential for practical applications in the physical world. Directly applying end-to-end reinforcement learning to high-frequency control tasks struggles with assigning credit to actions across long temporal horizons, compounded by the difficulty of efficient exploration. The alternative, learning low-frequency policies that guide higher-frequency controllers (e.g., proportional-derivative (PD) controllers), can result in a limited total expressiveness of the combined control system, hindering overall performance. We introduce EvoControl, a novel bi-level policy learning framework for learning both a slow high-level policy (using PPO) and a fast low-level policy (using Evolution Strategies) for solving continuous control tasks. Learning with Evolution Strategies for the lower-policy allows robust learning for long horizons that crucially arise when operating at higher frequencies. This enables EvoControl to learn to control interactions at a high frequency, benefitting from more efficient exploration and credit assignment than direct high-frequency torque control without the need to hand-tune PD parameters. We empirically demonstrate that EvoControl can achieve a higher evaluation reward for continuous-control tasks compared to existing approaches, specifically excelling in tasks where high-frequency control is needed, such as those requiring safety-critical fast reactions.

Constructing robust simulators is essential for asking “what if?” questions and guiding policy in critical domains like healthcare and logistics. However, existing methods often struggle, either failing to generalize beyond historical data or, when using Large Language Models (LLMs), suffering from inaccuracies and poor empirical alignment. We introduce G-Sim, a hybrid framework that automates simulator construction by synergizing LLM-driven structural design with rigorous empirical calibration. G-Sim employs an LLM in an iterative loop to propose and refine a simulator’s core components and causal relationships, guided by domain knowledge. This structure is then grounded in reality by estimating its parameters using flexible calibration techniques. Specifically, G-Sim can leverage methods that are both likelihood-free and gradient-free with respect to the simulator, such as gradient-free optimization for direct parameter estimation or simulation-based inference for obtaining a posterior distribution over parameters. This allows it to handle non-differentiable and stochastic simulators. By integrating domain priors with empirical evidence, G-Sim produces reliable, causally-informed simulators, mitigating data-inefficiency and enabling robust system-level interventions for complex decision-making.

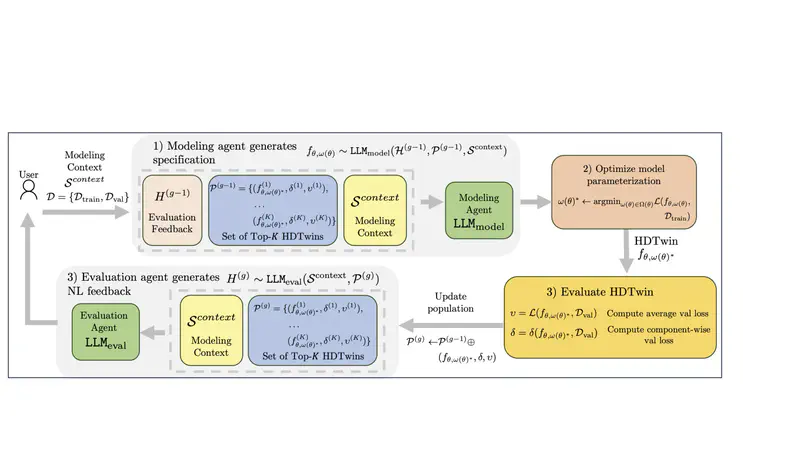
Hybrid Digital Twins (HDTwins) offer a novel approach to modeling dynamical systems by combining mechanistic and neural components, effectively leveraging domain knowledge while enhancing flexibility. However, existing hybrid models typically rely on manually defined architectures, limiting adaptability and generalization—particularly in data-scarce or unseen scenarios. To address this, we introduce HDTwinGen, an evolutionary algorithm that utilizes Large Language Models (LLMs) to autonomously generate, optimize, and refine hybrid digital twin architectures. Through iterative LLM-driven proposals and parameter optimization, HDTwinGen explores a vast design space, enabling the evolution of increasingly robust and generalizable HDTwins. Empirical results show that HDTwinGen surpasses conventional methods, yielding models that are not only sample-efficient but also adept at adapting to novel conditions, advancing the state of Digital Twin technology in dynamic real-world applications.

This work introduces Data-Driven Discovery (D3), a multi-agent framework that harnesses Large Language Models (LLMs) to iteratively propose, evaluate, and refine interpretable dynamical-system models—particularly in pharmacology but also applicable to fields like epidemiology. A central feature is its Value of Information (VoI) mechanism, which guides which new features or measurements to acquire for optimal model improvement, even when data for those features is not yet available. Crucially, D3 orchestrates three specialized LLM-driven agents—Modeling, Feature Acquisition, and Evaluation—in a closed loop, leveraging unstructured domain insights, selective data collection, and automated code generation. The resulting pipeline achieves robust modeling accuracy (often surpassing purely symbolic or purely black-box methods) while maintaining interpretability and efficient data usage, providing a compelling template for how LLM agents can collaborate on complex scientific workflows.

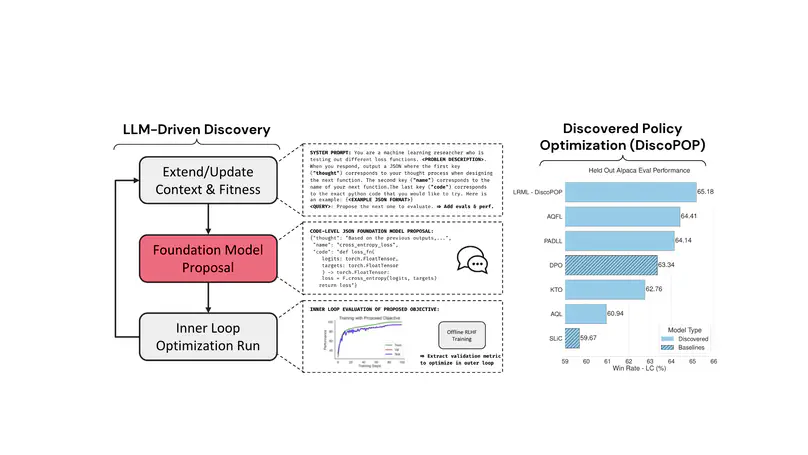
Offline preference optimization is a key method for enhancing and controlling the quality of Large Language Model (LLM) outputs. Typically, preference optimization is approached as an offline supervised learning task using manually-crafted convex loss functions. While these methods are based on theoretical insights, they are inherently constrained by human creativity, so the large search space of possible loss functions remains under explored. We address this by performing LLM-driven objective discovery to automatically discover new state-of-the-art preference optimization algorithms without (expert) human intervention. Specifically, we iteratively prompt an LLM to propose and implement new preference optimization loss functions based on previously-evaluated performance metrics. This process leads to the discovery of previously-unknown and performant preference optimization algorithms. The best performing of these we call Discovered Preference Optimization (DiscoPOP), a novel algorithm that adaptively blends logistic and exponential losses. Experiments demonstrate the state-of-the-art performance of DiscoPOP and its successful transfer to held-out tasks.

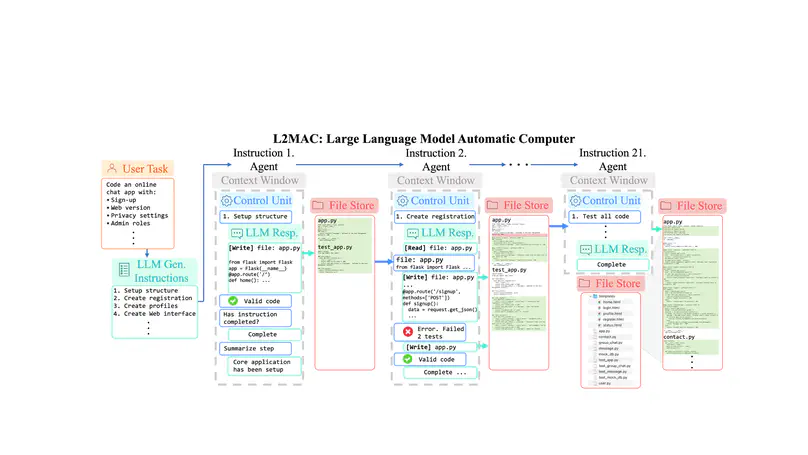
L2MAC is the first practical LLM-based stored-program automatic computer framework, suitable for generating unbounded, long, and consistent outputs. This framework, instantiated and demonstrated for large code base coding tasks, leverages an external memory comprised of a file store and instruction registry, as well as a control unit managing the context of the LLM. Consequently, it overcomes the limitation imposed by the fixed context window constraint inherent in transformer-based LLM architectures, outperforming other methods in generating large code bases for complex system design tasks.

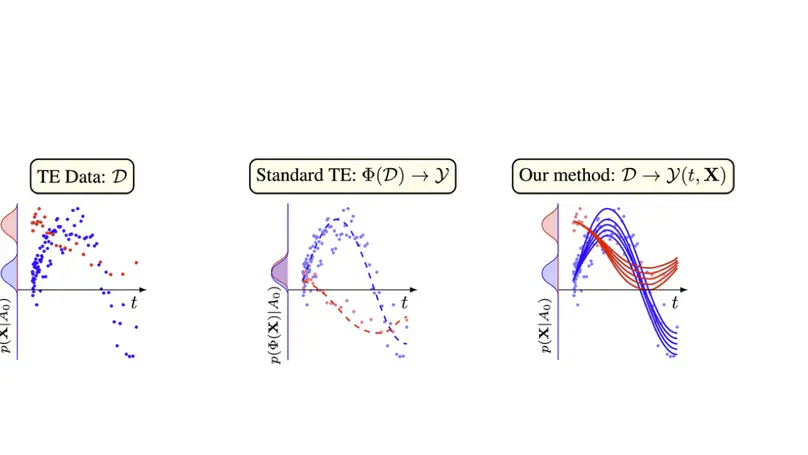
This paper presents a new approach to inferring unbiased treatment effects, using human-readable ordinary differential equations (ODEs) instead of traditional neural networks. This method enhances interpretability and accommodates irregular sampling, while introducing fresh identification assumptions. The innovation lies in transforming any ODE discovery into a treatment effects methodology, potentially revolutionizing the field.

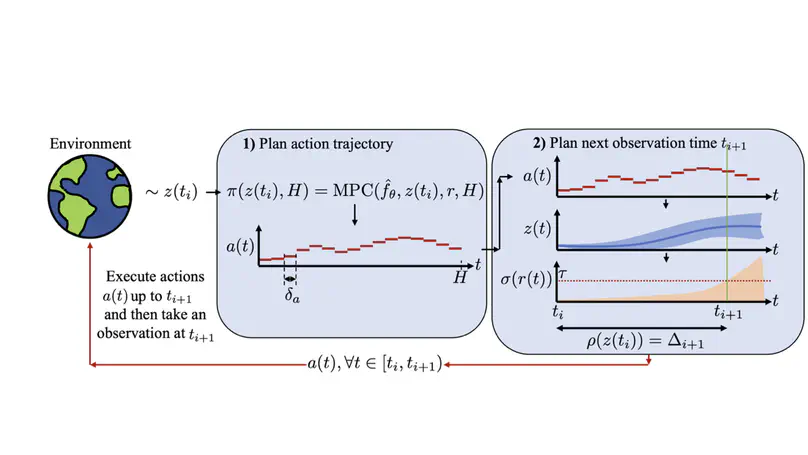
For the first time, we introduce and formalize the problem of continuous-time control with costly observations, theoretically demonstrating that irregular observation policies outperform regular ones in certain environments. We empirically validate this finding using a novel initial method: applying a heuristic threshold to the variance of reward rollouts in an offline continuous-time model-based Model Predictive Control (MPC) planner across various continuous-time environments, including a cancer simulation. This work lays the foundation for future research on this critical problem.

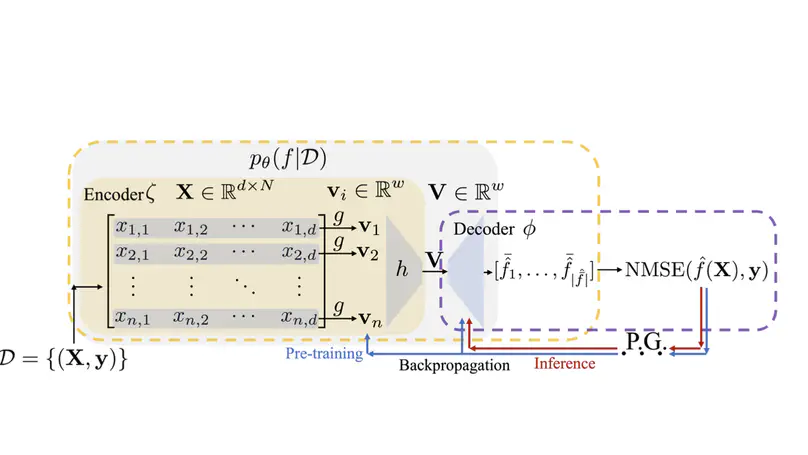
The problem of symbolic regression involves discovering concise, closed-form mathematical equations from data, a challenge due to its nature as a large-dimension combinatorial search problem. We propose a novel transformer architecture capable of encoding an entire dataset. This architecture can be trained end-to-end using the Root Mean Square Error (RMSE) of the fit of the generated equation, employing model-free reinforcement learning, specifically Proximal Policy Optimization (PPO) augmented with genetic programming to enhance sample diversity. Our method undergoes pre-training and is gradient fine-tuned at inference time to adapt to the dataset of interest. We designate this generative model as the Deep Generative Symbolic Regression (DGSR) framework. Through experiments, we demonstrate that DGSR not only achieves a higher recovery rate of true equations with a larger number of input variables but also offers greater computational efficiency at inference time compared to state-of-the-art reinforcement learning symbolic regression solutions.

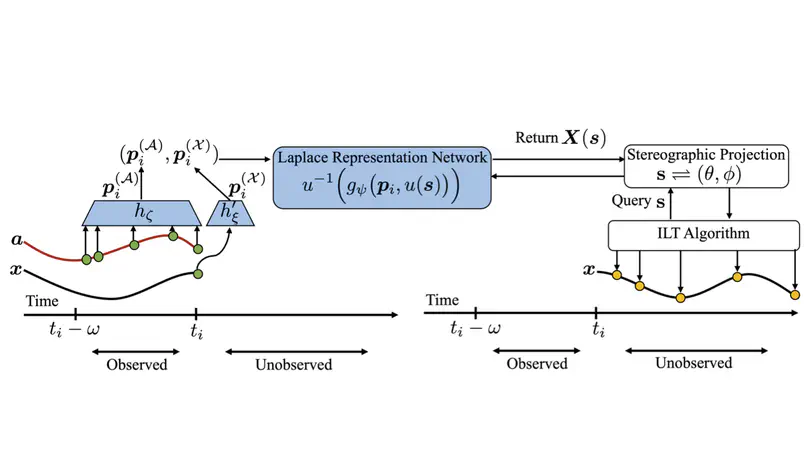
Many offline reinforcement learning (RL) problems in the real world, such as satellite control, encounter continuous-time environments characterized by irregular observation intervals and unknown delays affecting state transitions. These environments present significant challenges since current actions influence future states after an unpredictable delay. While existing offline RL algorithms perform well in environments with either irregularly timed observations or known delays, they fall short when both conditions are present. To address this issue, we introduce Neural Laplace Control, a continuous-time, model-based offline RL technique. This innovative approach combines a Neural Laplace dynamics model and a Model Predictive Control (MPC) planner, efficiently learning from datasets with irregular time intervals and inherent, constant unknown delays. Through experimental application in continuous-time delayed environments, Neural Laplace Control has demonstrated its ability to achieve performance levels near those of expert policies.

Neural Ordinary Differential Equations (ODEs) struggle to model systems with long-range dependencies or discontinuities common in engineering and biological contexts. Despite alternative approaches, numerical instability persists when handling stiff ODEs and those with piecewise forcing functions. This work introduces Neural Laplace, a framework adept at learning various classes of differential equations, efficiently representing history-dependencies and discontinuities in the Laplace domain through complex exponentials. By leveraging the geometric stereographic map of a Riemann sphere, Neural Laplace ensures smoother learning in this domain. Experimental results indicate its superior performance in modeling and extrapolating trajectories of diverse differential equations, even those with complex history dependencies and abrupt changes.